Uno de los conceptos que veremos con frecuencia en la creación de shaders son las matrices. Una matriz es una lista de elementos numéricos que siguen ciertas reglas aritméticas y son utilizadas a menudo en Computer Graphics.
En Unity las matrices representan una transformación espacial y entre ellas podemos encontrar:
- UNITY_MATRIX_MVP.
- UNITY_MATRIX_MV.
- UNITY_MATRIX_V.
- UNITY_MATRIX_P.
- UNITY_MATRIX_VP.
- UNITY_MATRIX_T_MV.
- UNITY_MATRIX_IT_MV.
- unity_ObjectToWorld.
- unity_WorldToObject.
Todas corresponden a matrices de cuatro por cuatro dimensiones, es decir que cada una posee cuatro filas y cuatro columnas de valores numéricos.
Su representación conceptual es la siguiente:
(
Xx, Yx, Zx, Tx,
Xy, Yy, Zy, Ty,
Xz, Yz, Zz, Tz,
Xt, Yt, Zt, Tw
);
Como ejemplificamos anteriormente en la sección 1.0.2; cuando hablamos de vértices, un objeto poligonal posee dos nodos por defecto. En Maya estos nodos son conocidos como Transform y Shape, y ambos se encargan de calcular la posición de los vértices en un espacio denominado Object-Space, el cual define la posición de los vértices en relación con la posición del centro del mismo objeto.
El valor final de cada vértice de un objeto es multiplicado por una matriz conocida como Model Matrix (UNITY_MATRIX_M), la cual nos permite modificar los valores de transformación, rotación y escala del mismo. Cada vez que rotamos, cambiamos de posición o escalamos nuestro objeto, el Model Matrix es actualizado.
¿Cómo ocurre este proceso? Para entenderlo vamos a suponer la transformación de un Cubo en nuestra escena. Iniciaremos tomando un vértice de nuestro Cubo que se encuentre en la posición 0.5X, -0.5Y, -0.5Z, 1.0W con respecto a su centro.
Cabe mencionar que el canal “W” corresponde a un sistema de coordenadas denominado homogéneo, el cual nos permite manejar vectores y puntos de manera uniforme. En las transformaciones de matrices, la coordenada W puede ser igual a cero o a uno. Cuando nW es igual a 1, se refiere a un punto en el espacio, mientras que, cuando es igual a 0, se refiere a una dirección.
Más adelante en este libro hablaremos de este sistema cuando multipliquemos vectores por matrices y viceversa.
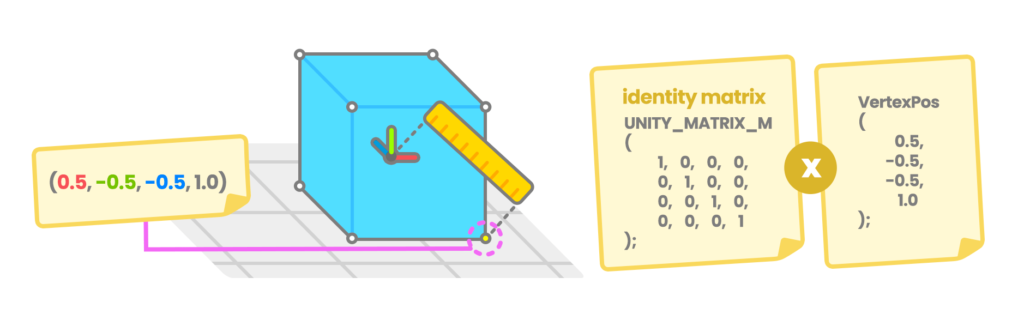
Uno de los elementos a considerar con respecto a las matrices es que una multiplicación se puede llevar a cabo siempre y cuando el número de columnas de la primera matriz sea igual al número de filas de la segunda. Como ya sabemos nuestro Model Matrix posee una dimensión de cuatro filas y cuatro columnas, y la posición de los vértices posee una dimensión de cuatro filas y una columna.
Como la cantidad de columnas en el Model Matrix es igual a la cantidad de filas en la posición de los vértices, podemos multiplicar y el resultado será igual a una nueva matriz de cuatro filas y una columna, lo que definiría una nueva posición para los vértices. Este proceso de multiplicación ocurre para todos los vértices en nuestro objeto y tal proceso es llevado a cabo en el Vertex Shader Stage.
Hasta este punto ya sabemos que Object-Space se refiere a la posición de un vértice según su propio centro, entonces, ¿Qué quiere decir World-Space, View-Space o Clip-Space? El concepto es básicamente el mismo.
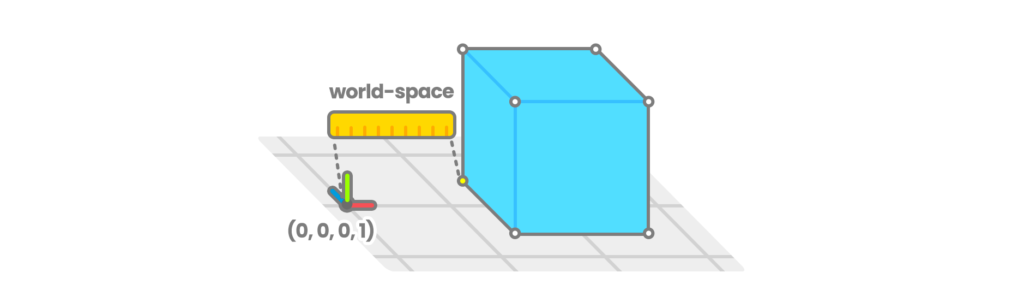
World-Space corresponde a la posición de un vértice según el centro del mundo; a la distancia entre el punto inicial de la cuadrícula en nuestra escena (0X, 0Y, 0Z, 1W) y la posición de un vértice en el objeto.
Si deseamos transformar una coordenada de espacio desde Object-Space a World-Space podemos utilizar la variable interna unity_ObjectToWorld.
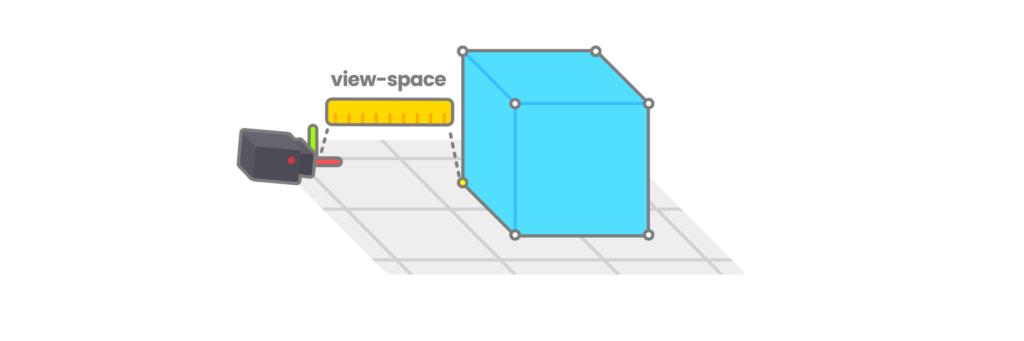
View-Space corresponde a la posición de un vértice de nuestro objeto con relación a la vista de la cámara. Si deseamos transformar una coordenada de espacio desde World-Space a View-Space podemos emplear la matriz UNITY_MATRIX_V.
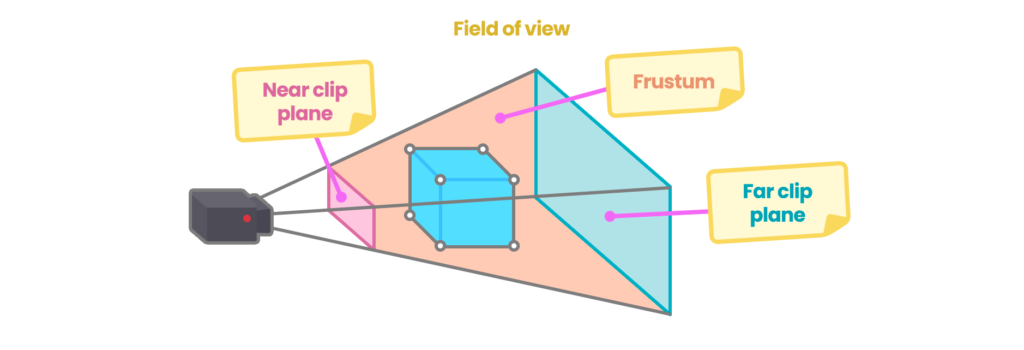
Finalmente, Clip-Space, también conocido como Projection-Space, se refiere a la posición de un vértice de nuestro objeto con relación al frustum de la cámara. Así pues, el factor será afectado por el Near Clipping Plane, Far Clipping Plane y Field of View.
Si deseamos transformar una coordenada de espacio desde View-Space a Clip-Space podemos utilizar la matriz UNITY_MATRIX_P.
En general, se ha definido a nivel conceptual las distintas coordenadas de espacio, pero aún no se ha precisado en sí a qué se refieren las matrices de transformación.
Por ejemplo, la variable interna UNITY_MATRIX_MVP se refiere a la multiplicación de tres matrices distintas. La letra M es igual a Model Matrix, V es igual a View Matrix y P es igual a Projection Matrix. Esta matriz se usa principalmente para transformar directamente los vértices de un objeto desde Object-Space a Clip-Space. Recordemos que nuestro objeto poligonal ha sido creado en un entorno tridimensional mientras que la pantalla de nuestro ordenador; en donde será proyectado, es bidimensional, por lo tanto, será necesario transformar nuestro objeto desde un espacio a otro.
Este concepto será discutido más adelante en el libro, cuando utilicemos la función UnityObjectToClipPos( VRG ), incluida en nuestro shader, dentro del Vertex Shader Stage.
